알고리즘과 시간 복잡도

2017-12-09

알고리즘
시간 복잡도
Big O 표기법
Asymptotic Complexity 점근적 분석
재귀함수

합 구하기
피보나치 수열

좋은 알고리즘의 필요 요건과, 알고리즘의 실행 속도를 평가하는 방법을 알아본다.

1. 알고리즘

우리는 finite amount of space and time에 집중해야한다.
알고리즘은 유한한 자원을 가진 환경에서 주어진 문제를 푸는 동작의 모임이다.
적은 시간과 적은 자원(공간)을 이용해 문제를 해결하는 알고리즘이 좋은 알고리즘이다.

+ 웹 브라우저에서 사용할 수 있는 메모리는 일반적인 데스크톱 애플리케이션의 가용 메모리에 비해 매우 적다. 적은 메모리만 할당받는 주된 이유는 웹 페이지에서 실행하는 자바스크립트가 시스템 메모리를 전부 사용해서 운영체제를 다운시키는 일을 방지하기 위함이다.
메모리 제한은 변수 할당 뿐만 아니라 호출스택, 스레드에서 실행할 수 있는 문장수에도 영향을 미친다.
즉! 가능한 최소한의 메모리만 사용해야 페이지의 성능을 올릴 수 있다.

예제_Facebook 친구 2명이 가진 공통 친구 리스트를 만드는 가장 빠르 방법은?

n명의 페이스북 친구를 가진 A와 m명의 페이스북 친구를 가진 B의 공통 친구의 수는

단순하게 생각한다면 n*m
800명, 400명이라면 320,000번의 비교로 찾을 수 있다.
시간복잡도를 배우고, 연산횟수를 줄이는 방법을 생각해보자.

2. 시간복잡도 +

시간복잡도란 알고리즘이 문제를 해결하기 위한 **시간(연산)의 횟수**를 말한다.
computational complexity that measures or estimates the time
taken for running an algorism.
Time complexity is commonly estimated by counting the number of elementary operations performed by the algorism, supposing that an elementary operation takes a fixed amount of time to perform.

알고리즘을 평가하는데 있어 수행시간과 메모리 사용량을 평가기준으로 두는데
수행시간에 해당하는 것이 시간 복잡도 Time Complexity,
메모리 사용량에 해당하는 것이 공간 복잡도 Space Complexity이다.

연산 횟수를 카운팅 할때 3가지 경우가 있다.

최선의 경우 Best Case
최악의 경우 Worst Case
평균적인 경우 Average Case

평균적인 경우가 가장 이상적으로 보이겠지만 알고리즘이 복잡해 질수록 평균적인 경우는 구하기가 매우 어려워 진다. 그러므로 최악의 경우로 알고리즘의 성능을 파악한다.

2-1. Program Step에서 Elementary Operation이란?

프로그램의 진행 정도를 나타내는 기본 단위이다.

대입연산
덧셈, 뺄셈, 곱셈, 나눗셈
비교구문
함수호출

즉, 알고리즘의 실행 순서를 따라가며 Elementary Operation이 일어나는 수를 측정한다.

2-2. 어떻게 카운팅할까.

전역변수를 이용하여 Elementary Operation을 카운팅한다.
각 실행문 별로 Step수와 실행 횟수를 분석한다.

2-2-1. 전역변수를 이용하여 Elementary Operation을 카운팅

let count = 0;
function sum(list, n) {
  let tempSum = 0; // 대입연산

  for (let i = 0; i < n; i++) {
    count++;   // loop 한번 돌 때마다
    tempSum += list[i];
    count++;  // 대입연산
  }
  count++;  // for loop 끝날 때 한번
  count++;  // return 수행
  return tempSum;
}

2-2-2. 각 실행문 별로 Step수와 실행 횟수를 분석한다.

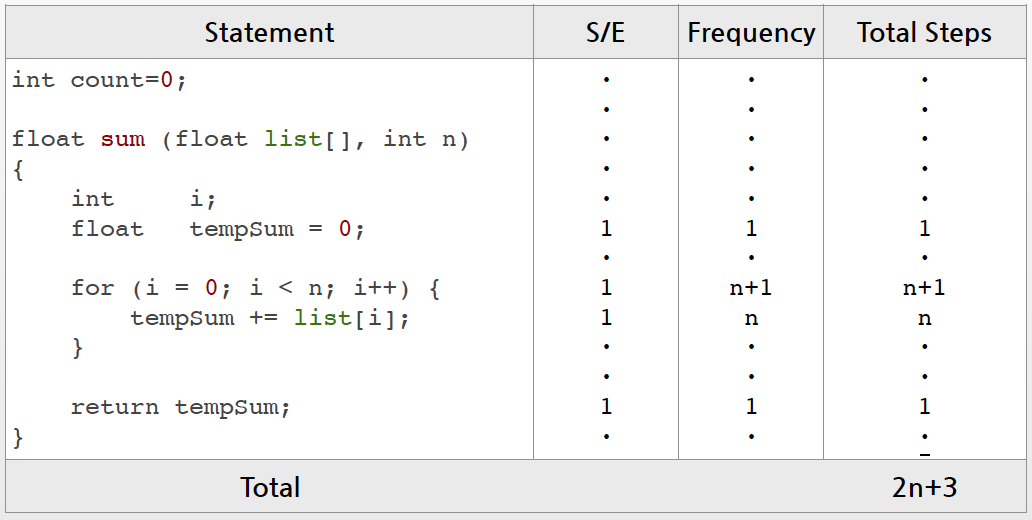
주어진 프로그램 2개의 성능 비교 및 분석

프로그램 P1의 성능 : C1 * n^2 + C2 * n
프로그램 P2의 성능 : C3 * n

C1, C2, C3에 따라서 대소 비교 결과가 다름.
어떤 C1, C2, C3에 대해서도 C1 * n^2 > C3 * n을 만족하는 n은 존재함.

n이 작으면 프로그램 P1의 성능이 더 좋을 수도 있다.
n이 충분히 크면 항상 프로그램 P2의 성능이 좋다. (P1에는 n이 제곱이기 때문에)

작은 경우 모두 성능이 좋으므로 문제될 것은 없다.
따라서 n이 큰 경우의 처리가 중요하다.

3. Big O 표기법

Big O가 중요한 이유를 알기 위해서는 Asymptotic Complexity에 대해 알야아한다.
알고리즘의 성능평가는 시간복잡도와 공간복잡도를 계산하고, 적 표기법으로 나타내면 된다.

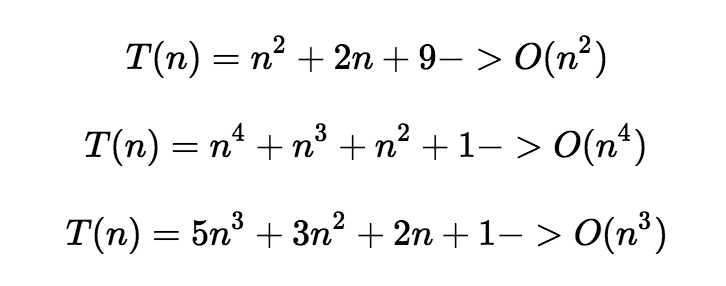
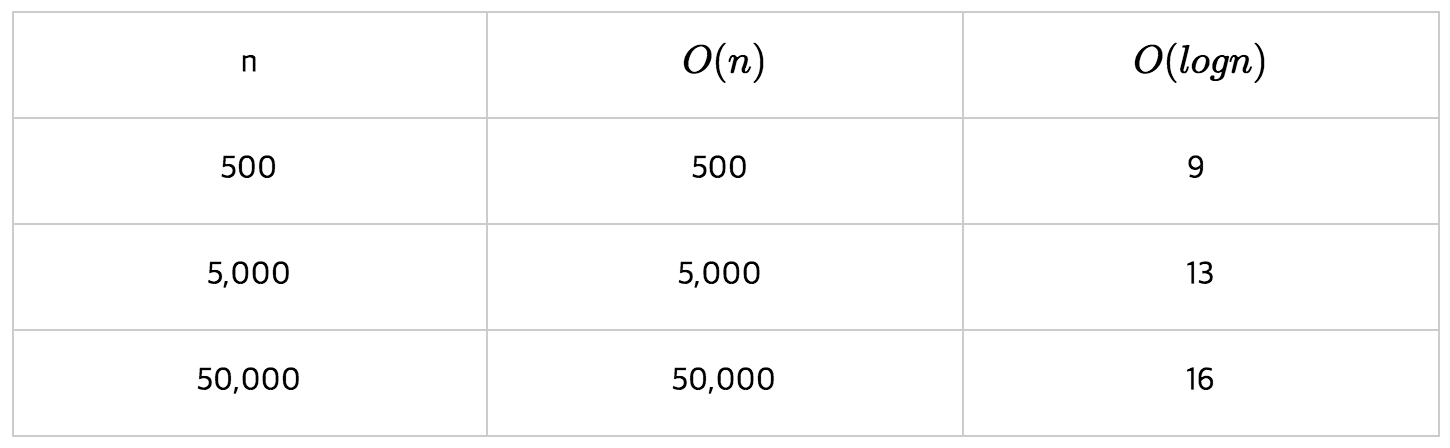
위 예와 같이 T(n)으로 표현한 함수의 최고차항의 차수가 빅오가 된다.
빅오의 순서는 아래와 같고 커질수록 좋지 않다.
보통 O(n^2)이상의 복잡도를 가지는 알고리즘은 좋지 않다.

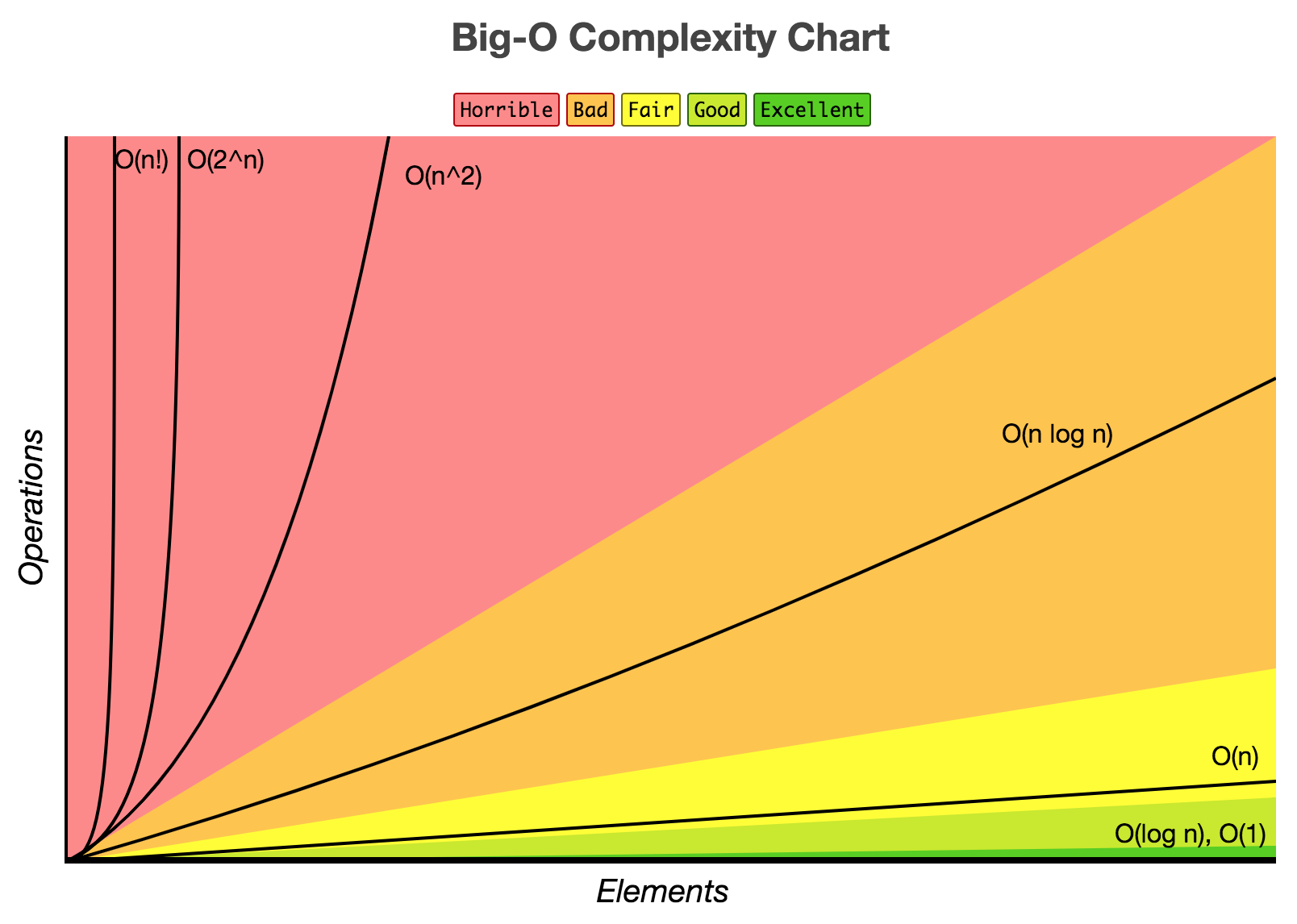
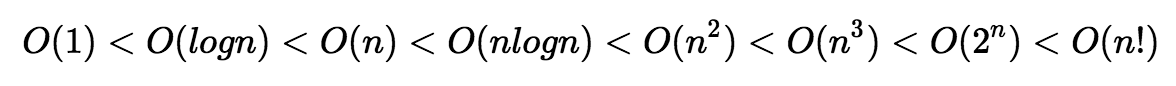
4. Asymptotic Complexity

입력의 크기가 충분히 클 때의 시간복잡도와 공간복잡도를 분석하는 것.

프로그램 성능이 Asymptotic(점진적인) Complexity

프로그램의 입력 크기 등 성능을 결정하는 주요 특성 값이 매우 클 때의 프로그램의 성능.
프로그램의 실행 속도가 어떤 경향을 가지는지를 평가한다고 생각하면 된다.
ex. 입력의 크기가 n이고 n이 매우 큰 경우
프로그램 성능 평가의 매우 중요한 기준.

4-1. 점근적 분석의 필요성

어떠한 문제 해결을 위한 알고리즘의 성능분석을 할 때, 주어지는 데이터의 형태나 실험을 수행하는 환경, 또는 실험에 사용한 시스템의 성능등 다양한 요소에 의해 공평한 결과가 나오기 힘들고 비교 결과가 항상 일정하지 않을 수 있다.

이를 효과적으로 해결하는 방법이 점근적 분석법이다. 점근적 분석법은 각 알고리즘이 주어진 데이터의 크기를 기준으로 수행시간 혹은 사용공간이 얼마나 되는지를 객관적으로 비교할 수 있는 기준을 제시해 준다.
O(빅오), Ω(오메가), Θ(세타)등이 있다. 일반적으로 빅오와 세타표기가 많이 사용된다.

4-2. 빅오 표기법 O Notation

점근적 상한선(Asymptotic upper bound)
주어진 알고리즘이 아무리 나빠도 비교하는 함수와 같거나 좋다.
정의 : O(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤f(n)≤cg(n) for all n≥n0} 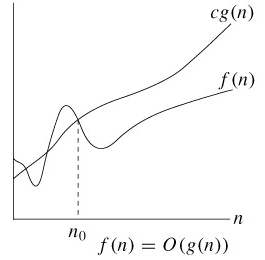n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 작거나 같다는 의미이다. 그래프가 아래에 있을 수록 수행시간이 짧은 것이므로 성능이 좋은 것이다.

4-3. 오메가 표기법 Ω Notation

점근적 하한선(Asymptotic lower bound)
주어진 알고리즘이 아무리 좋아도 비교하는 함수와 같거나 나쁘다.
정의 : Ω(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤cg(n)≤f(n) for all n≥n0} 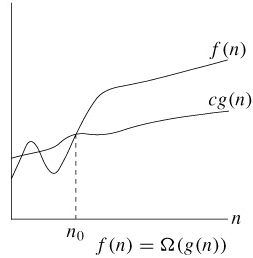n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 크거나 같다는 의미이다.

4-4. 세타 표기법 Θ Notation

점근선 상한선과 점근적 하한선의 교집합(Asymptotic tighter bound)
주어진 알고리즘이 아무리 좋아지거나 나빠지더라도 비교하는 함수의 범위안에 있다.
정의 : Θ(g(n)) = {f(n) : there exist positive constants c1, c2 and n0 such that 0≤c1g(n)≤f(n)≤c2g(n) for all n≥n0} 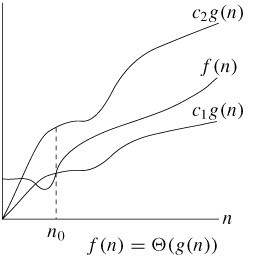n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 c1g(n)보다 크거나 같거나 c2g(n)보다 작거나 같다는 의미이다

cf. 의사코드란? pseudo-code +

의사(疑似: 비교할 의, 비슷할 사 | Pseudo: 가짜의- ) 코드는 컴퓨터 프로그램이나 알고리즘이 수행해야할 내용을 우리가 사용하는 언어 (한국어 또는 영어 등)로 간략히 서술해 놓은 것을 말합니다. 왜 의사코드를 사용해야 하나요?

의사코드는 코딩 입력을 시작하기 전, 사고를 좀더 명확히 정립하게 만들어주어 프로그램을 설계하는데 도움이 됩니다. 실제 코드 입력을 처음 시작할 때가 제일 힘듭니다! 단순히 소스코드를 입력하는 것보다 함수(function) 프로그램을 만들 때 많은 시간을 낭비할 수 있습니다. 약 10분 정도 각 풀이법의 장점과 단점을 주도면밀하게 살펴보면서 의사코드 작성한다면, 이후 디버그를 수정하고 코드를 재분해 하는데 걸리는 시간을 단축할 수 있습니다.

모델링이라고 생각해보자.

필오의 개발 docs ✨✊

01_Webzz. Algorithm